Fixed-income investors often ask what the duration of a bond is — as a way of determining interest rate sensitivity. Suppose the duration of a bond is five years1, this tells them that if rates go up 100 basis points (bps), the price will go down 5%. This is easy back-of-the envelope math that provides useful information; however, it ignores a key characteristic of the relationship between bond prices and yields — it is not a linear relationship. This approximation is fairly accurate for small moves in interest rates, but rate moves this year have been anything but small. The actual shape of the price/yield graph is convex, meaning it is curved.
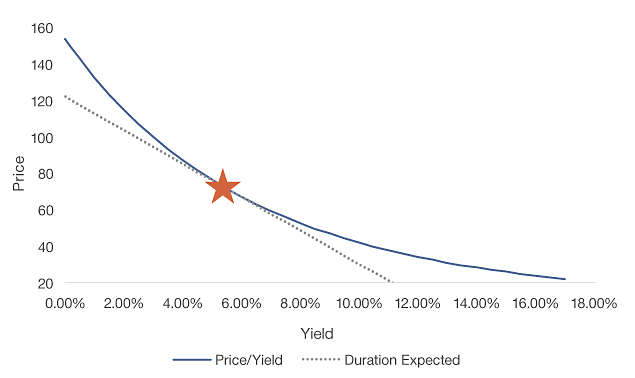
The chart below illustrates the relationship between price and yield of a U.S. Treasury Bond with a 3% coupon and 2042 maturity. Given a yield to maturity of 5.5%2, this bond has a duration of 12.8 years. The dotted line is the linear approximation of the price/yield relationship of the bond, as calculated using duration. For yields close to the 5.5% current level (notated by the star), there is little difference between the two lines. However, the further away the yield moves from the initial level, the greater variation there is between the linear approximation, or what is described below as “duration expected” and the actual curved line. The degree of curvature, which accounts for the error of the duration line, is known as “convexity.”
Duration alone does not explain the relationship between price and yield
Source: FactSet, as of 10/23/23
So the question becomes, why is there a variation between the lines? The answer is that duration is not static. Longer maturities, lower coupons and lower yields all equate to longer durations and vice versa. The duration expected line assumes a constant duration across all yields and is calculated using the current price and yield, which in this case is 71.7 and 5.5%, respectively. Because duration is actually longer at lower yields, investors have the potential to benefit from increased rate sensitivity when rates fall. Conversely, duration shortens as yields increase, which lessens the price impact of rising rates, again to the benefit of investors. This favorable attribute of bonds is known as positive convexity. Not only are prices greater than the linear approximation, but price increases at an accelerating rate and falls at a decelerating rate when a bond is positively convex. Put simply, bond prices go up faster than they come down.
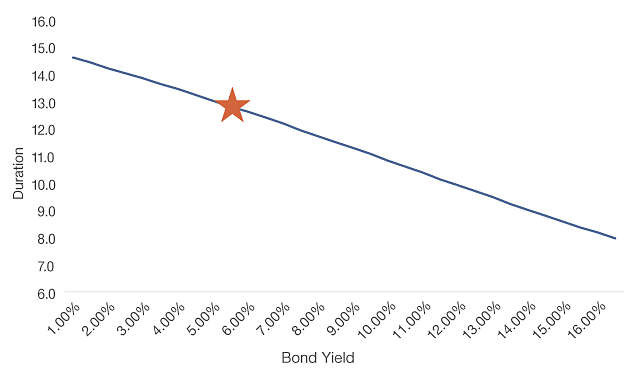
The chart below demonstrates the effect of convexity on duration. While duration measures the change in price given a change in yield, convexity accounts for the change in duration given that same change in yield. Bonds that exhibit positive convexity, like the one in this example, will have shorter durations at higher yields and longer durations at lower yields. The star reflects the current yield to maturity of 5.5% and 12.8 year duration. If Treasury yields continue to increase, the bond’s duration would decrease, mitigating some of the price decline. On the other hand, if yields decline, the bond’s price would increase at an accelerated rate as duration lengthens. It is important to note that certain bonds, such as mortgages and callable bonds, exhibit negative convexity at low yields. Using a callable bond as an example, the issuer can call the bond, which limits its price appreciation potential. 3 Graphically, the price/yield curve becomes concave at low yields, which, in the bond market, is referred to as negative convexity.
Duration changes in a favorable direction due to convexity
Source: FactSet, as of 10/23/23
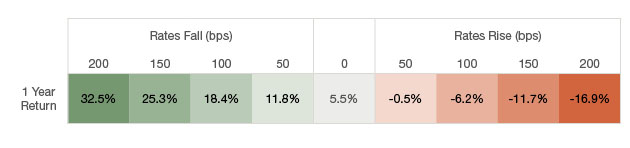
Sticking with the U.S. Treasury bond example, the following chart is a scenario analysis that calculates returns over a one-year time horizon, given changes in yield. Assuming a flat yield curve, or no change in yield, this bond would hypothetically earn 5.5% in the period. What is glaring about the analysis is the disproportionate upside in the case of falling rates, compared with the downside of continued rate increases. This asymmetrical return profile demonstrates the impact of positive convexity. It is important to note that shorter-maturity bonds, for example a 10-year U.S. Treasury or higher-coupon bond will have lower convexity and a less asymmetric return profile.
Positive convexity can lead to an asymmetric return profile
Source: FactSet. Hypothetical 1 year return given rate scenarios.
Duration is certainly an important measure and provides useful context regarding rate sensitivity. However, as demonstrated above, it may not always accurately predict expected returns when used alone. In fact when a bond exhibits positive convexity, its price will always be higher than the duration linear approximation. Therefore, when estimating a bond’s sensitivity to rates, there is a convexity adjustment added to the duration effect to better understand the bond’s potential price change. Since this adjustment is always positive, convexity leads to bond prices that go up faster than they come down.
1. Duration is a measure of the sensitivity of a fixed-income investment, such as a bond or a bond portfolio, to changes in interest rates.
2. Yield to maturity (YTM) is the overall interest rate earned by an investor who buys a bond at the market price and holds it until maturity.
3. Callable or redeemable bonds are bonds that can be redeemed or paid off by the issuer prior to the bonds' maturity date. When an issuer calls its bonds, it pays investors the call price (usually the face value of the bonds) together with accrued interest to date and, at that point, stops making interest payments.
About risk
Past performance is no guarantee of future results, which will vary. All investments are subject to market risk and will fluctuate in value.
Treasury Securities are backed by the full faith and credit of the United States government as to payment of principal and interest if held to maturity. Interest income on these securities is exempt from state and local taxes.
Bonds are subject to interest-rate risk and can lose principal value when interest rates rise. Bonds are also subject to credit risk, in which the bond issuer may fail to pay interest and principal in a timely manner, or that negative perception of the issuer’s ability to make such payments may cause the price of that bond to decline.
Diversification cannot assure a profit or protect against loss in a declining market.
Important disclosures
This material contains the opinions of its authors but not necessarily those of New York Life Investments or its affiliates. It is distributed for informational purposes only and is not intended to constitute the giving of advice or the making of any recommendation to purchase a product. The opinions expressed herein are subject to change without notice. The investments or strategies presented are not appropriate for every investor and do not take into account the investment objectives or financial needs of particular investors.
This material represents an assessment of the market environment as at a specific date, is subject to change, and is not intended to be a forecast of future events or a guarantee of future results. This information should not be relied upon by the reader as research or investment advice regarding any funds or any particular issuer/ security.
Any forward-looking statements are based on a number of assumptions concerning future events, and although we believe the sources used are reliable, the information contained in these materials has not been independently verified, and Its accuracy is not guaranteed. In addition, there is no guarantee that market expectations will be achieved.
New York Life Investments and its affiliates do not provide tax advice. You should obtain advice specific to your circumstances from your own legal, accounting, and tax advisors.
This material contains general information only and does not take into account an individual’s financial circumstances. This information should not be relied upon as a primary basis for an investment decision. Rather, an assessment should be made as to whether the information is appropriate in individual circumstances and consideration should be given to talking to a financial professional before making an investment decision.
By subscribing you are consenting to receive personalized online advertisements from New York Life Investments.
